Today we will dive into torch.autograd module, one of them most important under the hood PyTorch’s module. It implements automatic differentiation of arbitrary scalar valued functions.

Table of contents:

• How to calculate gradients ?
• How to locally disable gradients ?
• How to measure performance ?

How to calculate gradients ?

Torch.autograd performs automatic differentiation using two different modes: reverse mode and forward mode.

The popularity of reverse mode in deep learning comes from the fact that in general the input dimensionality is higher than the output dimensionality. But theorically, for any \(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\), the reverse mode should be used if and only if \(n>>m\), otherwise if \(n<<m\), forward mode is more performant.

The reason behind is the order we multiply Jacobian matrices in the chain rule. Indeed, considering real function f and g such that \(f: \mathbb{R}^{n_0} \rightarrow \mathbb{R}^{n_1}\) and \(g: \mathbb{R}^{n_1} \rightarrow \mathbb{R}^{n_2}\) where \((n_0,n_1,n_2) \in \mathbb{N}^3\). Then, if we consider the derivative of \(y= g \circ f\) on \(x \in \mathbb{R}^{n_0}\), we have:

In multi-dimensional space, the analogy of derivatives is the Jacobian matrix defined for any \(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\) by:

And the chain rule can be re-written, for any \(f: \mathbb{R}^{n_1} \rightarrow \mathbb{R}^{n_2}\) and \(g: \mathbb{R}^{n_0} \rightarrow \mathbb{R}^{n_1}\) two real functions, as:

This implies we can rewrite the Jacobian matrix of a composition as a product of two matrices. If we have a composition of several functions, we have to calculate a matrix product.

The optimised way of calculating the matrix product is not always straightforward, it depends on the dimensions of the matrix. If we multiply matrices from right to left, we perform forward AD, otherwise if we multiply matrices from left to right, we perform backward AD.

Example

Let us calculate the gradient of a two layer MLP written as functions defined by \(h=f_3 \circ f_2 \circ f_1\) where \(f_1: \mathbb{R}^{n_0} \rightarrow \mathbb{R}^{n_1}\), \(f_2: \mathbb{R}^{n_1} \rightarrow \mathbb{R}^{n_2}\) and \(f_3: \mathbb{R}^{n_2} \rightarrow \mathbb{R}^{n_3}\) such that:

Where:

We have:

Hence:

Using the chain rule,

So the Jacobian is the product of the three weight matrices. We can calculate it using from left to right product (reverse mode) or from right to left product (forward mode).

Reverse mode

In PyTorch, reverse mode automatic differentation is the by default mode. To calculate gradients, torch.autograd contains two main functions:

• backward(): convenient when working with a torch.nn model since it does not require the user to specify which Tensors we want the gradient for. It adds a .grad field to the leaf tensors.
• grad(): does not add a grad field and requires to specify the Tensors we want the gradients for.

Theory

To perform reverse AD, PyTorch records a computation graph containing all the operations to go from inputs to outputs. It gives us a directed acyclic graph whose leaves are the input tensors and roots are the output tensors. The graph is created in forward pass, while gradients are calculated in backward pass using the computation graph.

One important thing to note is that intermediary results are saved during the forward pass in order to execute the backward pass. Those intermediary tensors can increase GPU memory consumption on training.

Let us see an example with a simple linear layer. We use torchviz to visualize execution graphs and traces. This code must be launched in a notebook after having installed graphviz and torchviz.

sudo apt-get install graphviz   
pip install torchviz

# Imports:
import torch
from torch import nn
from torchviz import make_dot
from collections import OrderedDict

# Params
in_f, out_f=16,2

# Setup
x=torch.arange(in_f, dtype=torch.float32)
model=nn.Sequential(OrderedDict([ ('Lin1',nn.Linear(in_f,out_f)) ]) )

y=model(x)
make_dot(y.mean(), params=dict(model.named_parameters()), show_attrs=True, show_saved=True)

Blue boxes: represent tensors requiring a gradient computation. We can see the linear weight matrix of shape (2,16) and the linear bias matrix of shape (2).

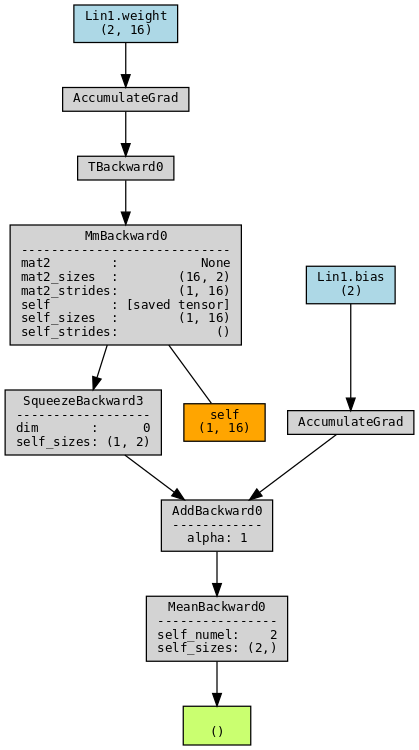
Orange boxes: represent intermediary tensors. Those are tensors saved during the forward pass that enables to calculate gradients during the backward.

Grey boxes: minimal transformations and traces. Let us explain some boxes:

• AccumulateGrad : indicates that gradients need to be calculated. Since weight and bias matrices are encoded as nn.Parameter, they have requires_grad set to True and appear in blue while the input has requires_grad set to False and does not appear;
• TBackward0 : refers to the transposed operation (W^T);
• MmBackward0: refers to the matrix multiplication (x.W^T);
• AddBackward0: refers to the addition (x.W^T + b);

Intermediary tensors imply additional memory cost during training. It is one possible reason explaining why a model fit in memory during evaluation and not during training. These intermediary results are packed during the forward pass (saved) and unpack during the backward pass (when access to the tensor is required). If we want to control the packing/ unpacking behaviour, we can use the torch.autograd.graph.saved_tensors_hooks() context manager.

# Call every time a tensor is saved: forward pass
def pack_hook(x):
    print(x)
    print("Packing", x.shape)
    return x

# Call every time a tensor is accessed: backward pass
def unpack_hook(x):
    print("Unpacking", x.shape)
    return x

with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    y=model(x) # Call pack_hook and defined unpack_hook
y.mean().backward() # Call unpack_hook

If this feature is useful for debugging and adds modularity but what is more interesting is to control wether the intermediary tensors are saved on the cpu or on the GPU because very often, the tensors involved in the computation graph live on GPU. Keeping a reference to those tensors in the graph is what causes most models to run out of GPU memory during training while they would have done fine during evaluation. If it is possible to do it using pack_hook, unpack_hook, PyTorch provides another context manager torch.autograd.graph.save_on_cpu(). During the forward pass, tensors will be stored on CPU, while during backward pass, they will be put to the GPU.

Example:

We continue the theorical example of the composition of three nested linear layers to verify that the Jacobian of the composition is the product of the weight matrices. To do this, we can either use the torch.autograd.grad() or torch.autograd.backward().

Let us begin with “backward”. According to the documentation, it computes the sum of gradients with respect to graph leaves. We note that it has an argument called grad_tensors specifying the gradient of the output. It multiplies the result on the left by grad_tensors. If we note it G and \(f\) the function we are calculating the jacobian, then the result will of torch.autograd.backward is: \(G . J_f\)

For instance, if \(G\) is equals to a tensor full of one, we have:

In practice,

# Imports:
import torch
from torch import nn

# Main:
in_f, inter_f, out_f=3,128,2

# Setup
x=torch.arange(in_f, dtype=torch.float32, requires_grad=True)
lin_in, lin_inter, lin_out=(nn.Linear(in_f,inter_f), 
                            nn.Linear(inter_f, inter_f), 
                            nn.Linear(inter_f, out_f))
model=nn.Sequential(lin_in, lin_inter, lin_out)

# Forward
y= model(x)
grad_output=torch.ones(out_f)

# Backward: sum of gradients
torch.autograd.backward(y, grad_tensors=grad_output)
jacob_sum=x.grad

# Sanity check
prod=lin_out.weight @ lin_inter.weight @ lin_in.weight # W_3.W_2.W_1
torch.allclose(jacob_sum, torch.sum(prod, dim=0)) # Equality !

The torch.autograd.grad() counterpart is really close to the previous implementation and rather straightforward:

# Change this
# torch.autograd.backward(y, grad_tensors=grad_output)
# jacob_sum=x.grad
# By
jacob_sum=torch.autograd.grad(y, x, grad_outputs=grad_output)

Forward mode

PyTorch 1.12 has a beta API implementing forward mode AD. It contains three main functions:

• foward_ad.dual_level(): a context manager ensuring that all dual tensors created inside will have their tangents destroyed upon exit. Convenient to avoid confusing tangents from different computations.
• foward_ad.make_dual(): create a dual tensor associating a primal tensor with a dual tensor. The name comes from the dual number theory.
• foward_ad.unpack_dual(): unpacks a dual tensor giving its Tensor value and its forward AD gradient.

Theory

We have already explained that the theorical difference between reverse and forward mode is the way we compute matrix product. In practice, we can not use the same pipeline, i.e create a computational graph and backpropagate. To implement forward AD, we need a bit of dual number theory.

Let us write any dual number \(x=a+b. \epsilon\) where \(\epsilon^2=0\). When we apply, for any real function, the Taylor series on a dual number, we have: \(f(a+b\epsilon)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a) b^n \epsilon^n }{n!} = f(a)+b.f^{'}(a).\epsilon\) since \(\epsilon^2=0\).

Hence, for any real function g, we have:

Moreover, we have for any real function f and g:

The previous results are sufficient to calculate derivatives. For instance, if \(f: \mathbb{R} \rightarrow \mathbb{R}\) such that \(\forall x \in \mathbb{R}, f(x)=x^2.sin(x)\). If we want to calculate the derivative on 3, we do the following calculus:

Hence,

Example

We use the same example as before and keep the notations of the official introductory notebook: primal (input, previously “x”) and tangent (input derivatives). Using the same notations as before, tangent T applies the following transformation on the Jacobian: \(J_f . T\)

Thus, if \(T\) is equals to a tensor full of one, we have:

import torch
from torch import nn

# Params
in_f, inter_f, out_f=3,128,2

# Setup
x=torch.arange(in_f, dtype=torch.float32)
tangent = torch.ones(in_f)
lin_in, lin_inter, lin_out=(nn.Linear(in_f,inter_f), 
                            nn.Linear(inter_f, inter_f), 
                            nn.Linear(inter_f, out_f))
model=nn.Sequential(lin_in, lin_inter, lin_out)

# Forward
with fwAD.dual_level():
    dual_input = fwAD.make_dual(x, tangent)
    y = model(dual_input)
    jvp = fwAD.unpack_dual(y).tangent

# Sanity check
prod=lin_out.weight @ lin_inter.weight @ lin_in.weight # W_3.W
torch.allclose(jvp, torch.sum(prod, dim=1)) # Equality !

The result is the same as before !

Reverse AD vs forward AD

In the introduction, I presented the interest of the AD forward method when the dimensionality of the output space is higher than that of the input space. It is time to verify the statement in coding.

N,M=1024,16

x=torch.randn(N)
model=nn.Linear(N,M)

# Forward AD
primal=x.clone()
tangents=torch.eye(N)

start=time.perf_counter()
jacob_fwd=[]
for tangent in tangents:
    with fwAD.dual_level():
        dual_input = fwAD.make_dual(x, tangent)
        y = model(dual_input)
        jvp = fwAD.unpack_dual(y).tangent
    jacob_fwd.append(jvp)
jacob_fwd=torch.stack(jacob_fwd)
end=time.perf_counter()

print(f'Forward AD: {end-start:>21.5f}s shape {jvp.shape}')

# Reverse AD
inp=x.clone().requires_grad_(True)
gradients=torch.eye(M)

start=time.perf_counter()
y=model(inp)
jacob_rev=[]
for grad in gradients:
    torch.autograd.backward(y, grad_tensors=grad, retain_graph=True)
    jacob_rev.append(inp.grad)
jacob_rev=torch.stack(jacob_rev)
end=time.perf_counter()
print(f'Backward AD: {end-start:>20.5f}s shape {inp.grad.shape}')

torch.allclose(jacob_rev, jacob_fwd.T)

One could use more advanced functions to criticise the use of ‘for’ loops. However, this code gives us a first impression of the time difference and is not intended to be as optimised as possible. Nonetheless, results are striking. The difference in computation time between the two approaches is of several magnitudes depending on whether the final dimension is greater than the initial one.

This result is very important because if I had said that the popularity of reverse AD in deep learning was due to the fact that the output dimension is usually smaller than the input dimension, there are problems and architectures (encoder) that do not verify this result.

One can hope that one day the optimisation will intelligently choose which mode to use according to the intermediate spaces of the architecture.

Optimized comparison

The last code snippet, give us a hint about the best mode depending on the situation. However, it was a bit tedious. That is why, PyTorch has implemented optimized functions in torch.autograd.functional to calculate Jacobians (1st order) and Hessians (2nd order) in a beta API. PyTorch is trying to catch up with JAX on the optimized calculation of high-order gradients.

Example:

For instance, instead of using a for loop to calculate jacobian, we can use a one-line function. The results are faster but the conclusion is the same: the time difference depends on the distance between the dimensions.

N,M=16,1024

x=torch.randn(N)
model=nn.Linear(N,M)

# Forward 
start=time.perf_counter()
jacob_fwd=torch.autograd.functional.jacobian(model, x, vectorize=True, strategy='forward-mode')
end=time.perf_counter()
print('Time: {:10.3f}'.format(end-start))

# Reverse
start=time.perf_counter()
jacob_rev=torch.autograd.functional.jacobian(model, x)
end=time.perf_counter()
print('Time: {:10.3f}'.format(end-start))

torch.allclose(jacob_rev, jacob_fwd)

How to locally disable gradients ?

There are two common situations where we want to disable gradients: during inference or using custom code. Different context manager help us to globally disable or enable gradient calculation and storage. There are three different context:

• grad mode: it is the by default mode and is the only mode in which requires_grad takes effect. It is used when training models.
• no-grad mode (torch.set_grad_enabled(False) or torch.no_grad()): convenient to temporary disable the tracking of any operations requires to latter calculate gradients without having to set requires_grad to False and then back to True.
• inference mode (torch.inference_mode()): optimized version of no-grad mode disabling view tracking and version counter bumps. It is used in during data processing and evaluation.

Note:

• model.eval() is not a context manager. It only change the behaviour of modules acting differently during training and evaluation (nn.Dropout, nn.BatchNorm2d)
• None of the context manager is available for forward AD.

How to measure performance ?

Profiling

Profiling code is really important to optimize code, find bottlenecks, check GPU memory, check CPU memory, etc. PyTorch has implemented a profiler recording GPU and CPU events with a simple context manager torch.autograd.profiler.profile(). Originally it was part of torch.autograd module since it deals with code optimisation. But, with PyTorch 1.8.1 release, the module is considered legacy and is deprecated in favour of torch.profiler module.

Autograd profiler has many interesting arguments such as:

• enabled: allows to enable or not profiling. It is useful so that we do not have to comment on or uncomment the code, whether we want to profile it or not.
• use_cuda: enables timing of CUDA event.

in_f, out_f=128,1
bool_profile=False

# Setup
x=torch.arange(in_f, dtype=torch.float32, requires_grad=True)
model=nn.Sequential(nn.Linear(in_f,out_f))

with torch.autograd.profiler.profile(enabled=bool_profile) as prof:
    for _ in range(10):
        y=model(x)       

if prof is not None:
    # Save profiling
    prof.export_chrome_trace('result_profiling')

    # Print table order by CPU time 
    print(prof.key_averages().table(sort_by="self_cpu_time_total"))

After profiling, we can print table in the terminal directly using a simple print or after having grouped functions using profiler.profile.key_averages. Another intersting tools is to save a trace of the profiling and to load it later in: chrome://tracing

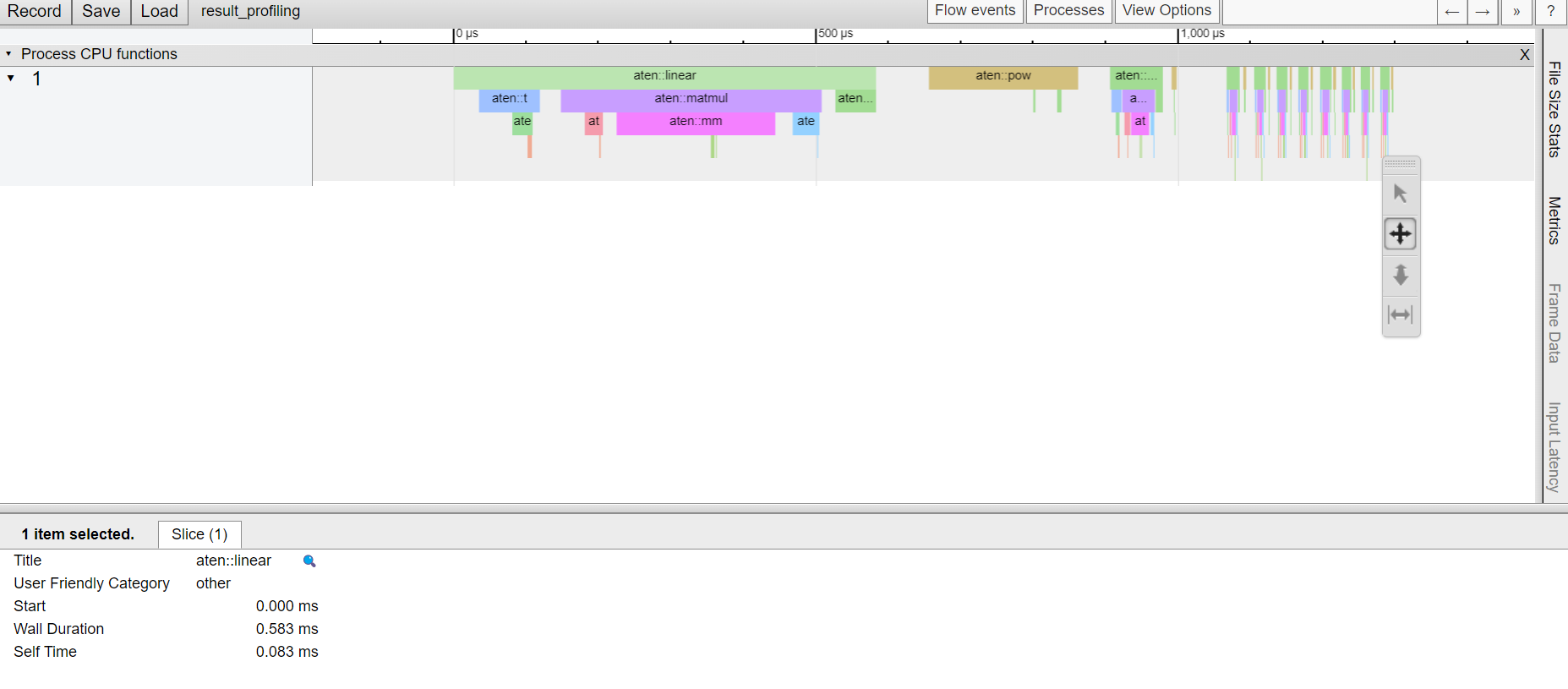
Ressources

Concepts:

• AD
• Understand AD
• Understand AD (2)
• Mathematical aspects of AD

Benchmark:

• Comparison between AD modes
• AD mode time comparison

Notebooks:

• AD
• Autograd
• Autograd Hooks

News:

• Profiler